Poster un message

1 2 3 4 5 6 7 8 9 ... 22 23

La science dont se targuent essentiellement ces architectes-ingénieurs du moyen âge, c’est la géométrie. On tente souvent de caractériser cette géométrie qui est la leur, en disant que, contrairement à celle d’Euclide, elle ne comporte pas de démonstrations. Mais là n’est pas le problème.

Il existe, au moye âge, tout un courant de géométries pratiques issu, tout à la fois, des agrimenseurs romains et des usages de l’astrolabe ou du cadran. Ces traités n’ont généralement pas de démonstrations et pourtant, ils sont tout différents de ce l’on trouve, par exemple, chez Villard de Honnecourt et son continuateur le Maitre II. Chez ces derniers, la géométrie se ramène à des sortes de recettes purement visuelles et opératoires, qui excluent, non seulement les démonstrations, mais surtout aussi les calculs. Comme symbole de cet état d’esprit, j’ai reproduit la représentation de ԉ chez Matthäus Roriczer (Fig. 1).

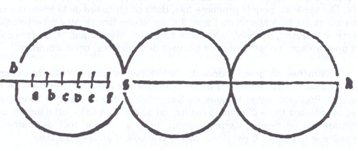
Fig. 1 ԉ Selon Matthäus Roriczen.

J’ai jadis, en 1963, eu l’occasion d’étudier ce qui se passa, en 1391, sur le chantier du Dôme de Milan. Il s’agissait d’élever l’édifice de telle manière que le faîte de l’église soit le sommet d’un triangle équilatéral dont la base serait la largeur du monument. Concrètement, il s’agissait de calculer la hauteur d’un triangle équilatéral de base 96. Face à un tel problème, les ingénieurs (inzignerii dans le texte) sont obligés de faire appel à un « expert en l’art de géométrie », Gabriel Stornaloro de Plaisance. De ce calcul, le grand historien d’art Erwin Panofsky avait proposé une reconstitution extrêmement compliquée et tirée par les cheveux. Comme le secret des alchimistes ou le secret des grandes découvertes maritimes, le prétendu « secret des maîtres d’œuvres » semble souvent rendre acceptables les divagations scientifiques les plus extravagantes. Dans le cas de la cathédrale de Milan, était, en fait, simplement appliquée la formule courante au moyen âge, selon laquelle la hauteur d’un triangle équilatéral est les 26/30 de sa base. Mais encore une fois, ce calcul, les ingénieurs n’avaient pas su le faire et ils avaient dû appeler à leur secours un géomètre expert. Si la géométrie des architectes ingénieurs du XIIIe siècle ne calculait pas, elle savait, en revanche, tirer de divers instruments, en particulier de l’équerre, des ressources restées, jusqu’il y a peu, insoupçonnées. Regardez l’équerre à bords non parallèles, dont l’architecte de Reims, Hughes Libergier avait fait tracer les contours sur sa propre tombe. Une corde tendue selon l’hypoténuse semble fournir les deux angles formés par la diagonale d’un rectangle dont les deux côtés ont entre eux la proportion du nombre d’or (Fig. 2).

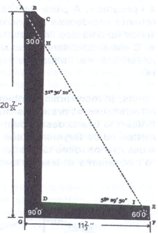
Fig. 2 Equerre de Hugues Libergier, architecte de Reims (XIIIe siècle) selon les contours tracés sur sa tombe.

On retrouve chez Villard de Honnecourt, plusieurs de ces équerres à bords non parallèles. Elles pouvaient, à la fois, servir à la taille des voussoirs et permettre, en l’absence de rapporteur à cette époque, l’obtention directe d’angles et de rapports privilégiés. Cependant, entre de telles pratiques et les Elements d’Euclide, le rideau de fer est peut-être moins infranchissable qu’on le dit. C’est du moins, ce que j’ai pensé lorsque, ayant découvert, à Salamanque, la Mathematica d’un savant toulousain du XIVe siècle, Philippe Eléphant, j’ai été amené à m’intéresser aux curieuses dénominations parfois attribuées au moyen âge, à certaines figures des Eléments d’Euclide. Regardez les figures baptisées « Victoire » et « Figure du Démon » (Fig. 3).

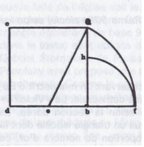
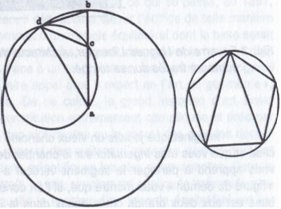
Fig. 3. Les figures « Victoire » et « Figure de Démon »

1 2 3 4 5 6 7 8 9 ... 22 23